Phương trình đường thẳng - Bài tập phần 11
B. \( \left[\begin{split} &2x + 2y - z- 6 = 0 \\ &2x + 3y - 2z - 7 = 0 \end{split} \right. \)
C. \( \left[\begin{split} &2x - y + 2z - 3 = 0 \\ &2x + 11y - 10z - 15 = 0 \end{split} \right. \)
D. \( \left[\begin{split} &2x - y + 2z - 1 = 0 \\ &2 - 3y + z + 6 = 0 \end{split} \right.\)

Đáp án:
Cách 1: Thử !!!
\( \vec{n}_Q = (1,-2,-2) \)
\( M(1,3,2) \).
Chọn \( N \) sao cho \( \overrightarrow{MN} = \vec{n}_Q \Rightarrow N(2,1,0) \)
Mp \( P: ax + by + cz + d = 0 \).
Vì \( d(O,(P)) = 1 \Rightarrow d \neq 0 \). Chọn \( d = 1 \).
Mp \( P: ax + by + cz + 1 = 0 \).
- Mp \( P \) qua \( M(1,3,2) \Rightarrow a + 3b + 2c + 1 = 0 \)
- Mp \( P \) qua \( N(2,1,0) \Rightarrow 2a + b + 1 = 0 \)
- \( d(O, (P)) = 1 \Rightarrow \frac{1}{\sqrt{a^2 + b^2 + c^2}} = 1 \)
Tóm lại:
\( \begin{cases} a + 3b + 2c + 1 = 0 \\ 2a + b + 1 = 0 \\ a^2 + b^2 + c^2 = 1 \end{cases} \Leftrightarrow \begin{cases} b = -1 - 2a \\ c = \frac{1}{2}(-1 - a - 3b) = \frac{1}{2}(5a + 2) \\ a^2 + (-1 - 2a)^2 + \frac{1}{4} (5a + 2)^2 - 1 = 0 \end{cases}\) (*)
(*) \(\Rightarrow 45a^2 + 36a + 4 = 0 \Rightarrow \begin{cases} a = -\frac{2}{3}, b = \frac{1}{3}, c = -\frac{2}{3} \\ a = -\frac{2}{15}, b = -\frac{11}{15}, c = \frac{10}{15} \end{cases}\)
Mp \( P: \left[\begin{split} &2x - y + 2z - 3 = 0 \\ &2x + 11y - 10z - 15 = 0 \end{split} \right. \Rightarrow \boxed{C}\)
B. \( a - 2b + c - 3d = 0 \)
C. \( 5a + 10b + 6c + 4d = 0 \)
D. \( 2a - 13b + 5c - 4 = 0 \)
Đáp án:
Chọn \(\boxed{C}\)
page52
(Đề 2018 câu 37, Mã 101)

Đáp án:
- Chọn hệ trục \( Ixyz \) như hình vẽ, xem cạnh hình vuông \( a = 1 \).
- \( M(0, 0, \frac{1}{6}), D'(\frac{\sqrt{2}}{2}, 0, 0), C'(0, \frac{\sqrt{2}}{2}, 0) \).
- Pt mp \((MC'D')\): \( \frac{x}{\frac{\sqrt{2}}{2}} + \frac{y}{\frac{\sqrt{2}}{2}} + \frac{z}{\frac{1}{6}} = 1 \Rightarrow \sqrt{2}x + \sqrt{2}y + 6z - 1 = 0. \)
\( A(0, -\frac{\sqrt{2}}{2}, 1) \Rightarrow \overrightarrow{AM} = (0, \frac{\sqrt{2}}{2}, -\frac{5}{6}) \)
\( B(-\frac{\sqrt{2}}{2}, 0, 1) \Rightarrow \overrightarrow{BM} = (\frac{\sqrt{2}}{2}, 0, -\frac{5}{6}) \)
\( \vec{n}_{(MAB)} = [\overrightarrow{AM}, \overrightarrow{BM}] = \left( \frac{-5\sqrt{2}}{12}, \frac{-5\sqrt{2}}{12}, -\frac{1}{12} \right), \vec{n}_{(MCD)} = (\sqrt{2}, \sqrt{2}, 6) \)
\( \cos \psi = \frac{|\vec{n}_{(MAB)} \cdot \vec{n}_{(MCD)}|}{|\vec{n}_{(MAB)}| |\vec{n}_{(MCD)}|} = \frac{\left| \frac{-10}{12} - \frac{10}{12} - 3 \right|}{\sqrt{\frac{136}{12}} \sqrt{40}} = \frac{56}{\sqrt{136 \times 40}} \)
\( \cos \varphi = \frac{7}{\sqrt{85}} = \frac{7\sqrt{85}}{85} \Rightarrow \boxed{B}. \)
page53
* Chú ý! Các tính chất cần đặc biệt chú ý để viết phương trình của đường thẳng:
\begin{cases}
\Delta \text{ qua } A \\
\Delta \perp d
\end{cases}
\Rightarrow \Delta \subset \text{mp}(P) \text{ qua } A \text{ và } \text{mp}(P) \perp d
\)
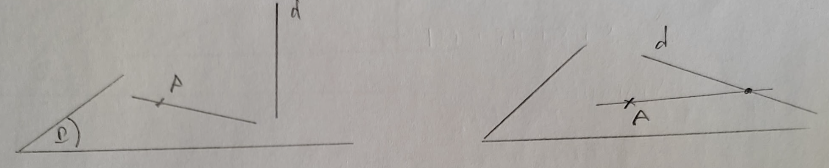
\begin{cases}
\Delta \text{ qua } A \\
\Delta \text{ cắt } d
\end{cases}
\Rightarrow \Delta \subset \text{mp}(A, d)
\)
\begin{cases}
\Delta \text{ qua } A \\
\Delta \parallel \text{mp}(Q)
\end{cases}
\Rightarrow \Delta \subset \text{mp}(P) \text{ qua } A \text{ và } \text{mp}(P) \parallel \text{mp}(Q)
\)

\begin{cases}
\Delta \text{ cắt } d_1 \\
\Delta \parallel d_2
\end{cases}
\Rightarrow \Delta \subset \text{mp}(P) \text{ chứa } d_1 \text{ và } \text{mp}(P) \parallel d_2
\)
page54
\begin{cases}
\Delta \text{ cắt } d \\
\Delta \perp \text{mp}(P)
\end{cases}
\Rightarrow \Delta \subset \text{mp}(Q) \text{ chứa } d \text{ và } \text{mp}(Q) \perp \text{mp}(P).
\)

\begin{cases}
d \perp \vec{a} \\
d \perp \vec{b}
\end{cases}
\Rightarrow \vec{u}_d = [\vec{a}, \vec{b}].
\)
page55
* Bài toán cơ bản (Giảng lại bài này để các bài toán sau chỉ nêu kết quả!)
\( (P): x - 3y + 2z - 1 = 0 \), \( (Q): 2x + y - 2z + 3 = 0 \)
có phương trình là:
B. \( \frac{x}{4} = \frac{y + 1}{6} = \frac{z - 2}{7} \)
C. \( \frac{x}{4} = \frac{y - 1}{6} = \frac{z - 3}{7} \)
D. \( \frac{x}{6} = \frac{y - 1}{4} = \frac{z - 2}{7} \)

Đáp án:
Đường thẳng \( \Delta \) qua \( (0,1,2) \in (P) \cap (Q) \):
\( \begin{cases} \Delta \perp \vec{n}_P \\ \Delta \perp \vec{n}_Q \end{cases} \Rightarrow \vec{u}_\Delta = \left[\begin{split} \vec{n}_P = (1, -3, 2) \\ \vec{n}_Q = (2, 1, -2) \end{split} \right] = (4, 6, 7) \)
Phương trình \( \Delta \): \( \frac{x}{4} = \frac{y - 1}{6} = \frac{z - 2}{7} \Rightarrow \boxed{A}. \)
page56