Đáp án:

\( M(x, y, z) \Rightarrow \overrightarrow{MA} = (1 - x, -y, -z), \overrightarrow{MB} = (2 - x, 1 - y, 3 - z), \overrightarrow{MC} = (-x, 2 - y, -3 - z) \)

\( MA^2 + 2MB \cdot MC = 8 \)

\(\Leftrightarrow (1 - x)^2 + y^2 + z^2 + 2(2 - x)(-x) + 2(1 - y)(2 - y) + 2(3 - z)(-3 - z) = 8 \)

\( \Leftrightarrow x^2 + y^2 + z^2 + 1-  2x + 2x^2 - 4x + 2y^2 - 6y + 4 + 2z^2 - 12z + 18 = 8 \)  

\( \Leftrightarrow 3x^2 + 3y^2 + z^2 - 6x - 6y - 21 = 0 \).  

\( \Leftrightarrow x^2 + y^2 + z^2 - 3x - 2y  - 7 = 0 \quad (S) \).  

Mặt cầu \( (S') \) có tâm \( I(1, -1, 0) \), bán kính \( R = \sqrt{1+1+7} =3 \).  

Mặt cầu \( (S) \) có tâm \( I(3, -1, 0) \), bán kính \( R = 3 \).  

\( IJ = \sqrt{4 + 4 + 1} = 2\sqrt{2} \).  

\(r = HM = \sqrt{MI^2 - IH^2} = \sqrt{9 - 2} = \sqrt{7} \Rightarrow \boxed{A}\)

page32

Đáp án:

\( M(x_0, y_0, z_0) \) thỏa: \( x_0 + 2y_0 + 2z_0 - A = 0 \).

 Nên \(M \in  mp(P): x + 2y + 2z - A = 0 \). Vậy \( M \) là điểm chung của \( (S) \) và \( (P) \).  

 Mặt cầu \( (S) \) có tâm \( I(2, 1, 1) \) và \( R = 3 \).  
\( (S) , (P) \) có điểm chung \( \Leftrightarrow d(I, (P)) \leq 3 \).  
 \(  \Leftrightarrow \frac{|6 - A|}{3} \leq 3  \Leftrightarrow -3 \leq A \leq 15 \).  

Min\( A = -3 \Leftrightarrow M \) là tiếp điểm của \( (S) \) và \( (P) \).  
\( x_0 + 2y_0 + 2z_0 + 3 = 0 \).  
\( M \) là hình chiếu vuông góc của \( I(2, 1, 1) \) lên mặt phẳng \( (P): x + 2y + 2z + 3 = 0 \).  
\(\Leftrightarrow M(1, -1, -1) \Rightarrow x_0 + y_0 + z_0 = -1  \Rightarrow \boxed{B}\).  

Cách 2:
\( A- 6 = (x_0 - 2) + 2(y_0 - 2) + 2(z_0 - 2) \).  

\( \leq \sqrt{(1 + 4 + 4)[(x_0 - 2)^2 + (y_0 - 2)^2 + (z_0 - 2)^2]} = 9 \)  
\( \Rightarrow -3 \leq A \leq 15 \).

page33

Đáp án:

- Mặt cầu \( (S) \) qua \( A \) và \( B \)  \(\Rightarrow\) Tâm \( I \) của mặt cầu \( (S) \) nằm trong mặt phẳng \( (Q) \), qua \( J(2, 2, 2) \bot \overrightarrow{AB} = (2, 0, 2) \).  
Phương trình mặt phẳng \( (Q): x + z - 4 = 0 \).  

- Suy ra: Tâm \( I \) của mặt cầu \( (S) \) nằm trên đường thẳng \( \Delta \) là giao tuyến của mặt phẳng \( (P) \) và \( (Q) \):  
\( \begin{cases} x - y - 3 = 0 \\ x + z - 4 = 0 \end{cases} \).

\( R = IA = \sqrt{JA^2 + IJ^2} \)

- \( R \) nhỏ nhất \(\Leftrightarrow IJ \) nhỏ nhất \(\Leftrightarrow I \) là hình chiếu vuông góc của \( J(2, 2, 2) \) xuống đường thẳng \( \Delta \).

\( \overrightarrow{u_\Delta} = [\overrightarrow{n_P}, \overrightarrow{n_Q}] = [(1, -1, 0), (1, 0, 1)] = (-1, -1, 1) \)

Mặt phẳng \(T\) qua \( J(2, 2, 2) \) vuông góc với \( \Delta \) có phương trình: \( x + y - z - 2 = 0 \).

Hình chiếu vuông góc của \( J \) xuống \( \Delta \) có tọa độ thỏa hệ:  
\( \begin{cases} x - y = 3 \\ x + z = 4 \\ x + y - z = 2 \end{cases} \Leftrightarrow I(3, 0, 1) \Rightarrow R = IA = 2\sqrt{2} \Rightarrow \boxed{D}\).

Cách 2: 
\( R = d(J, \Delta) = \sqrt{6} \Rightarrow R = \sqrt{JA^2 + IJ^2} = \sqrt{6 + 2\sqrt{2}} \)

page34

Đáp án:

Gọi \( D \) là điểm hợp lý
\( T = 3(\overrightarrow{MD} + \overrightarrow{DA})^2 + 2(\overrightarrow{MD} + \overrightarrow{DB})^2 + (\overrightarrow{MD} + \overrightarrow{DC})^2 + 3\overrightarrow{DA}^2 + 2\overrightarrow{DB}^2 + \overrightarrow{DC}^2 \) 
\( = 6MD^2 + 6\overrightarrow{MD} \cdot \overrightarrow{DA} + 4\overrightarrow{MD} \cdot \overrightarrow{DB} + 2\overrightarrow{MD} \cdot \overrightarrow{DC} + \dots \)
\( = 6MD^2 + 2\overrightarrow{MD} \cdot (3\overrightarrow{DA} + 2\overrightarrow{DB} + \overrightarrow{DC}) + \dots \)

Tìm điểm \( D \) sao cho: \( 3\overrightarrow{DA} + 2\overrightarrow{DB} + \overrightarrow{DC} = \overrightarrow{0} \).  
Gọi \( D(\alpha, \beta, \delta) \), ta có hệ:  
\( \begin{cases} 3( - \alpha) + 2(3 - \alpha) + ( - \alpha) = 0 \\ 3(1 - \beta) + 2( - \beta) + (21 - \beta) = 0 \\ 3(1 - \delta) + 2(-1 - \delta) + (-19 - \delta) = 0 \end{cases}  \Rightarrow \begin{cases} \alpha = 1 \\ \beta = 4 \\ \delta = -3 \end{cases} \Rightarrow D(1, 4, -3) \)

Mặt cầu \( (S) \) có tâm \( I(1, 1, 1) \) và \( R = 1 \).  

\( ID = \sqrt{9 + 16} = 5 \).  

\( T = 6MD^2 \) nhỏ nhất \(\Leftrightarrow DM \) nhỏ nhất:  
\( \begin{cases} DM = DI - R = 5 - 1 = 4 \\ M  \text{ là giao điểm của đường thẳng}  DI  \text{và mặt cầu} (S) \end{cases}\)  

Đường thẳng \( DI \):  \( \begin{cases} x = 1 \\ y = 1 + 3t \\ z = 1 - 4t \end{cases} \).  

 \( (1 - 1)^2 + (3t)^2 + (4t)^2 = 1  \Rightarrow 25t^2 = 1 \Leftrightarrow t = \pm \frac{1}{5} \)

 \(  M_1(1, \frac{8}{5}, \frac{1}{5}), M_2(1, \frac{2}{5}, \frac{9}{5}) \)

\( DM_1 = \sqrt{\frac{144}{25} + \frac{256}{25}} = 4 \Rightarrow M(1, \frac{8}{5}, \frac{1}{5}) \).  

\( \Rightarrow a + b + c = 1 + \frac{8}{5} + \frac{1}{5} = \frac{14}{5} \Rightarrow \boxed{D}\).

page35

Đáp án:

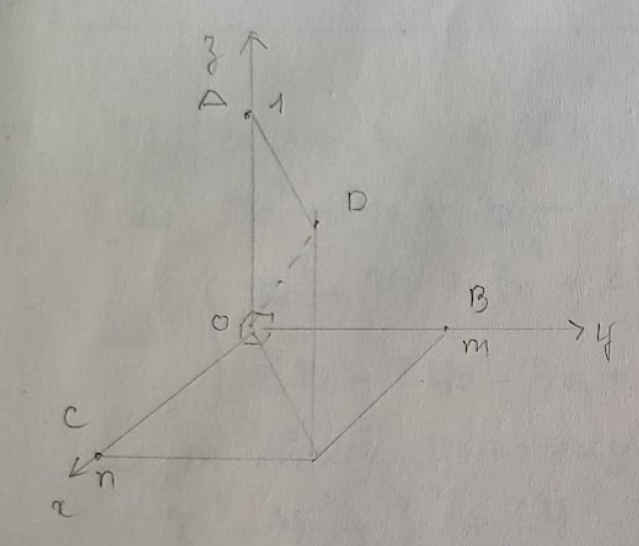
Gọi \( D(n, m, 1) \).  
Tâm mặt cầu ngoại tiếp tứ diện \( OABC \) là tâm mặt cầu ngoại tiếp hình hộp có chứa các đỉnh \( O, A, B, C \), \( I \) là trung điểm của \( OD \): \( I\left(\frac{n}{2}, \frac{m}{2}, \frac{1}{2}\right) \).  

Bán kính \( R \) của mặt cầu là: \( R = \frac{1}{2} \sqrt{n^2 + m^2 + 1} \)

\( 1 = m + 2n \leq \sqrt{5(m^2 + n^2)} \Rightarrow m^2 + n^2 \geq \frac{1}{5}\)

\( R = \frac{1}{2} \sqrt{m^2 + n^2 + 1} \geq \frac{1}{2} \sqrt{\frac{1}{5} + 1} = \frac{\sqrt{30}}{10} \)

\( \Rightarrow \min R = \frac{\sqrt{30}}{10} \Rightarrow \boxed{C} \)

(Dấu "=" xảy ra khi: \(m = \frac{n}{2}, \, n = 2m \Rightarrow \begin{cases} m = \frac{1}{5} \\ n = \frac{2}{5} \end{cases} \))

page36